Рекурсия. Быстрые сортировки. Сортировка подсчетом
Рекурсия вокруг нас
Если рассматривать понятие общо, то рекурсия – это ситуация, когда объект является частью себя.
Например, при демонстрации экрана на камеру в прямом времени. Ведь тогда камера снимает экран, на котором видно экран, на котором видно экран, на котором видно экран и так далее. Это пример бесконечной рекурсии.
Еще один пример бесконечной рекурсии – это фрактал – самоподобный объект. Например, так выглядит треугольник Серпинского:

 Итерации при построении треугольника Серпинского
Итерации при построении треугольника Серпинского
В математики последовательности можно задать рекуррентной формулой. Например, известная нам последовательность Фибоначчи задается именно таким образом:
\[ \begin{cases} F_1 = 1 \\ F_2 = 1 \\ F_n = F_{n - 1} + F_{n - 2}, n > 2 \end{cases} \]
Рекурсия в программировании
Рекурсия в программировании – вызов функции из нее же самой. Чаще всего применяется в:
- обработке графов (не будет рассмотрено в нашем курсе) – запускаем функцию из некоторой вершины. Она запускает себя же от соседней вершины. Так возникает рекурсия
 Обход графа в глубину – DFS
Обход графа в глубину – DFS
генерации перестановок, всех слов в алфавите. Почему? Если мы хотим все слова длины \(n\), то их можно получить, подставив все возможные буквы к каждому из слов длины \(n - 1\) – снова возникла рекурсия
сортировки. Чтобы отсортировать массив длины \(n\), можно разбить его на 2 половины и отсортировать каждую из них, а затем некоторым образо их совместить.
более сложные случаи применения рекурсии, которые не будут разбираться на курсе. Например, рекурсия может использоваться при построении выпуклой оболочки набора точек
Что общего у основных случаев рекурсии? Это сведение большой задачи к нескольким таким же подзадачам на меньших данных.
Нахождение суммы рекурсивно
Перейдем к более конкретным примерам и рассмотрим нахождение суммы элементов массива с помощью рекурсивной функции.
- Как разбить задачу на подзадачи? Заметим, что сумма массива длины \(n\) – это сумма первого элемента и всех остальных (то есть суммы массива длины \(n - 1\)). Более формально:
\[ \sum_{i = 1}^{n} a_i = a_1 + \sum_{i = 2}^{n} a_i = a_1 + \left( a_2 + \sum_{i = 3}^{n} a_i \right) = a_1 + (a_2 + (a_3 + \dots \ ) \dots ) \]
Тогда пусть \(\operatorname{sum}(i, j)\) – сумма элементов от \(i\)-того до \(j\)-того включительно. Тогда можем записать сумму следующим образом:
\[ \operatorname{sum}(i, j) = a_i + \operatorname{sum}(i + 1, j) \]
- Когда рекурсия должна остановиться? Это очень важный вопрос, ведь иначе рекурсия будет запускаться бесконечно, чего мы не хотим. Очевидный случай суммы массива – это когда массив состоит из одного элемента. Действительно, тогда этот единственный элемент и является всей суммой. Запишем это в нашу рекурсию:
\[ \operatorname{sum}(i, j) = \begin{cases} a_i + \operatorname{sum}(i + 1, j), \text{\ если \ } i \ne j \\ a_i, \text{\ если \ } i = j\pm \end{cases} \]
Затетим, что условие выхода (а именно его мы сейчас определили) может быть различным, например, такое задание рекурсии также будет корректно работать:
\[ \operatorname{sum}(i, j) = \begin{cases} 0, \text{\ если \ } i > j \\ a_i + \operatorname{sum}(i + 1, j), \text{\ иначе \ } \end{cases} \]
#include <iostream>
#include <vector>
int recursive_sum(const std::vector<int>& nums, int start, int stop) {
std::cout << "finding sum of " << start << " to " << stop << '\n';
if (start == stop) {
std::cout << "found sum of " << start << " to " << stop << ": " << nums[start] << '\n';
return nums[start];
}
std::cout << "finding sum of " << start << " to " << stop << " by summing " << start
<< " and sum of " << start + 1 << " to " << stop << '\n';
return nums[start] + recursive_sum(nums, start + 1, stop);
}
int main() {
std::vector<int> nums = {1, 2, 3, 4};
std::cout << recursive_sum(nums, 0, nums.size() - 1) << '\n';
return 0;
}finding sum of 0 to 3
finding sum of 0 to 3 by summing 0 and sum of 1 to 3
finding sum of 1 to 3
finding sum of 1 to 3 by summing 1 and sum of 2 to 3
finding sum of 2 to 3
finding sum of 2 to 3 by summing 2 and sum of 3 to 3
finding sum of 3 to 3
found sum of 3 to 3: 4
10Последнее замечании – о применимости такого рекурсивного подхода. Можно заметить, что так можно применять любую ассоциативную функцию (на итог выражения с которой не влияет расстановка скобок: \(a + b + c = (a + b) + c = a + (b + c)\) ). К таким можно отнести, например, операцию взятия максимума:
\[ \max (a, b, c) = \max (\max(a, b), c) = \max (a, \max(b, c)) \]
Общая рекомендация при работе с рекурсией
Для корректного написания рекурсии нужно:
свести задачу к набору меньших подзадач, после решения которых можно простым действием перейти к ответу на исходную задачу
проследить за ходом рекурсии и определить условие выхода – это тот примитивный случай, когда для ответа запуск рекурсии не требуется
проверить, что рекурсия всегда попадает в одно из условий выхода
Для облегчения рассуждений, можно считать, что функция уже написана и является черным ящиком – мы так делали, когда только начинали работать с функциями. Написав функцию, мы не думали о ее реализации, а просто использовали в остально программе как “черный ящик”. Здесь можно применить похожее рассуждение, только уже при написании самой функции. Например, в реализованной выше фукции recursive_sum(begin, end) мы верили, что она как-то находит сумму, и смело запускали ее на меньшем массиве, веря в корректную работу.
Рекурсия при работе с цифрами числа
Найдем максимальную цифру числа.
Сведение к подзадачам
Максимальная цифра всего числа: найдем максимум из последней цифры числа и максимумом из всех остальных цифр.
Более формально, \(\operatorname{max\_digit}(N) = \max (N \% 10, \operatorname{max\_digit}(N / 10))\), где \(\%\) и \(/\) – взятие остатка и целочисленное деление соответственно
Условие выхода
Если перед нами число из одной цифры, то она и будет наибольшей среди всех цифр этого числа.
Алгоритм Евклида
источник описания алгоритма Евклида
Классический алгоритм, который можно решать с помощью рекурсии – это алгоритм Евклида для нахождения НОД двух чисел (наибольшего общего делителя).
Наибольшим общим делителем (англ. greatest common divisor) целых неотрицательных чисел \(a\) и \(b\) называется наибольшее число \(x\), которое делит одновременно и \(a\), и \(b\). Когда оба числа равны нулю, результат не определён — подойдёт сколько угодно большое число. За исключением этого случая, верно следующее наблюдение: если одно из чисел равно нулю, то их \(\gcd\) равен второму числу.
Алгоритм нахождения
Алгоритм Евклида находит \(\gcd\) двух чисел \(a\) и \(b\) за \(O(\log \min(a, b))\), основываясь на следующей несложной формуле:
\[ \gcd(a, b) = \begin{cases} a, & b = 0 \\ \gcd(b,\, a - b), & b > 0 \end{cases} \]
Здесь предполагается, что \(a > b\).
Докажем корректность этой формулы:
Если \(g = \gcd(a, b)\) делит и \(a\), и \(b\), то их разность \((a-b)\) тоже будет делиться на \(g\).
Никакой больший делитель \(d\) числа \(b\) не может делить число \((a-b)\): если \(d > g\), то \(d\) не может делить \(a\), а значит и не делит \((a - b)\).
Прямая рекурсивная реализация:
int gcd(int a, int b) {
if (a < b) {
std::swap(a, b);
}
if (b == 0) {
return a;
}
return gcd(b, a - b);
}Этот алгоритм может работать долго — например, на паре \((10^9, 1)\) он сделает миллиард итераций.
Идея дальнейшей оптимизации в том, чтобы вычитать из \(a\) не одно \(b\) за раз, а столько, чтобы в следующий раз \(a\) и \(b\) уже поменялись местами — чтобы новое \(b\) стало меньше нового \(a\). Простой способ этого достичь — просто вычесть \(b\) из \(a\) сразу максимально возможное число раз, то есть взять вместо нового \(b\) остаток от деления \(a\) на \(b\):
\[ \gcd(a, b) = \begin{cases} a, & b = 0 \\ \gcd(b,\, a \bmod b), & b > 0 \end{cases} \]
В современном C++ есть встроенная библиотечная функция std::gcdиз хэдера <numeric>, которую рекомендуется использовать, не забывая про случай отрицательных чисел и \((0, 0)\). Эта функция уже могла использоваться на курсе в одной из домашних задач.
Время работы
Можно показать, что каждые две итерации меньшее число уменьшится хотя бы в два раза, а следовательно алгоритм работает за \(O(\log \min (a, b))\). Эта оценка относится не только к худшему случаю, но и к среднему.
Также иногда полезно знать, что нахождение \(\gcd\) группы из \(n\) чисел от \(1\) до \(A\) будет работать не за \(O(n \log A)\), а за \(O(n + \log A)\) — это несложно доказать по индукции.
Ханойские башни
Ханойская башня — перестановочная головоломка в виде трёх стержней, на один из которых в виде пирамиды нанизаны восемь колец разного диаметра. Задача состоит в том, чтобы переместить пирамиду из колец на другой стержень за наименьшее число ходов. За один раз разрешается переносить только одно кольцо, причём нельзя класть большее кольцо на меньшее.
Рекурсивное решение для произвольного количества колец
Рекурсивно решаем задачу «перенести башню из \(n−1\) диска на \(2\)-й стержень». Затем переносим самый большой диск на \(3\)-й стержень, и рекурсивно решаем задачу «перенеси башню из \(n−1\) диска на \(3\)-й стержень».
Отсюда методом математической индукции заключаем, что минимальное число ходов, необходимое для решения головоломки, равно \(2^n − 1\), где \(n\) — число дисков.
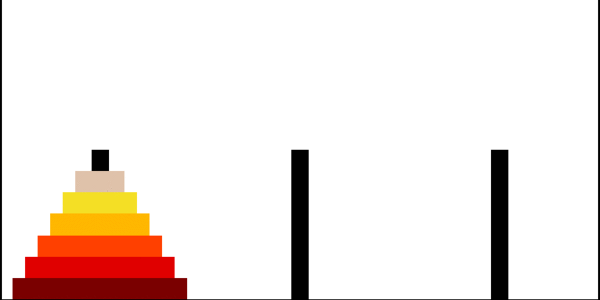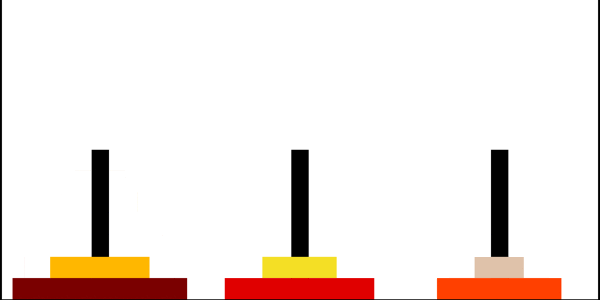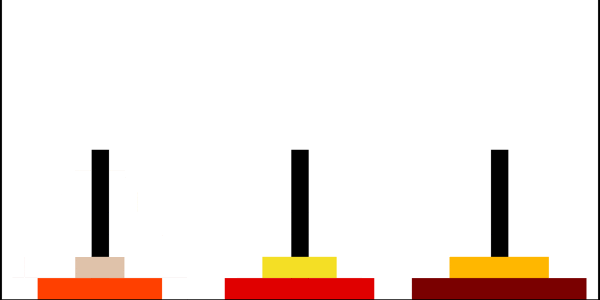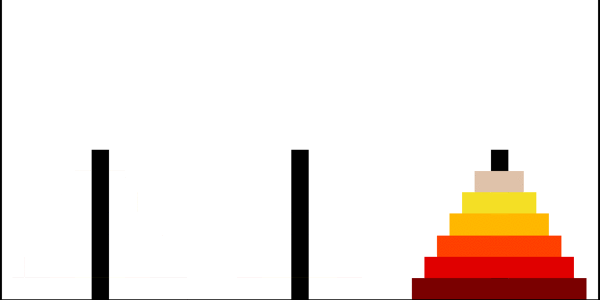 ы
ы
Оптимальные сортировки
Можно ли сделать сортировку быстрее, чем \({\cal{O}(n^2)}\)? Конечно.
Если у нас определена только операция “меньше”, то мы не можем обойтись без \({\cal{O}(n \log n)}\) операций. Докажем это.
Введем понятие дерева решений. Дерево решений – это бинарное дерево, в котором каждый узел представляет собой сравнение двух элементов массива. В каждом узле дерева находится подмножество множества всех перестановок на n элементов.
В корне дерева находится множество всех перестановок.
Каждый узел дерева представляет собой сравнение двух элементов массива. Если \(a_i < a_j\), то мы идем в левое поддерево, иначе – в правое. В корне левого поддерева находятся все перестановки, в которых \(a_i < a_j\), а в корне правого поддерева – все перестановки, в которых \(a_i > a_j\).
Каждый лист дерева представляет собой одну из возможных перестановок
Значит, в таком дереве будет \(n!\) листьев, так как у нас есть n элементов и \(n!\) возможных перестановок.
Поскольку дерево бинарное, то высота дерева будет равна \(\log_2(n!)\).
Оценим снизу высоту дерева:
\[ h = \log_2(n!) = \log_2 (n^n + \bar{o}(n^{n - 1})) \ge \log_2(n^n) = n \log_2(n) \]
Поскольку, высота дерева равна количеству сравнений, то мы получаем нижнюю оценку на сложность сортировки:
\[ \Omega \left( n \log_2(n) \right) \]
Сортировка слиянием (merge sort)
Сортировка слиянием – это алгоритм вида “разделяй и властвуй”, который разбивает массив на две половины до тех пор, пока каждая половина не станет размером в один элемент. Затем он объединяет эти половины обратно вместе в отсортированном порядке.
Введем вспомогательную операцию слияния двух отсортированных массивов. Эта операция принимает два отсортированных массива и объединяет их в один отсортированный массив. Это легко можно сделать, если создать два указателя, которые будут указывать на начало каждого массива. Затем мы будем сравнивать элементы, на которые указывают указатели, и добавлять меньший элемент в результирующий массив. После этого мы будем двигать указатель на массив, из которого был взят элемент. Когда один из массивов будет полностью обработан, мы просто добавим оставшиеся элементы другого массива в результирующий массив.
Алгоритм слияния (псевдокод)
function merge(arr1, arr2):
merged = []
i = 0
j = 0
пока i < len(arr1) И j < len(arr2):
если arr1[i] < arr2[j]:
merged.append(arr1[i])
i += 1
иначе:
merged.append(arr2[j])
j += 1
добавляем оставшиеся элементы из arr1 и arr2 в merged, если они есть
возвращаем mergedДалее будем работать по следующей схеме:
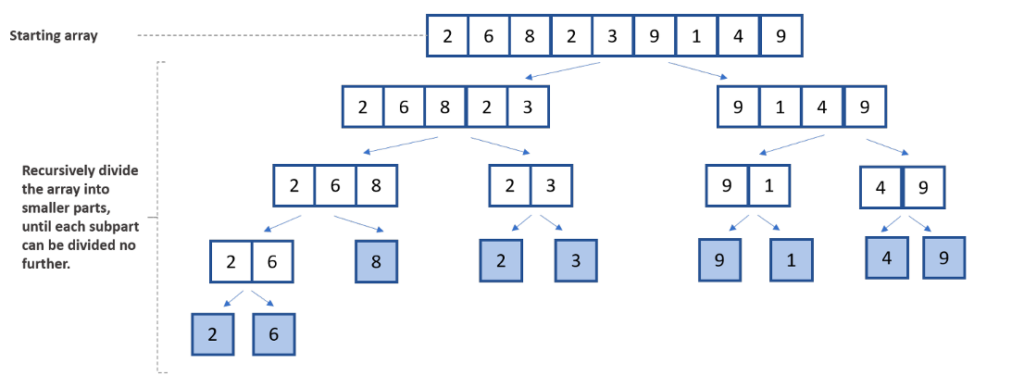
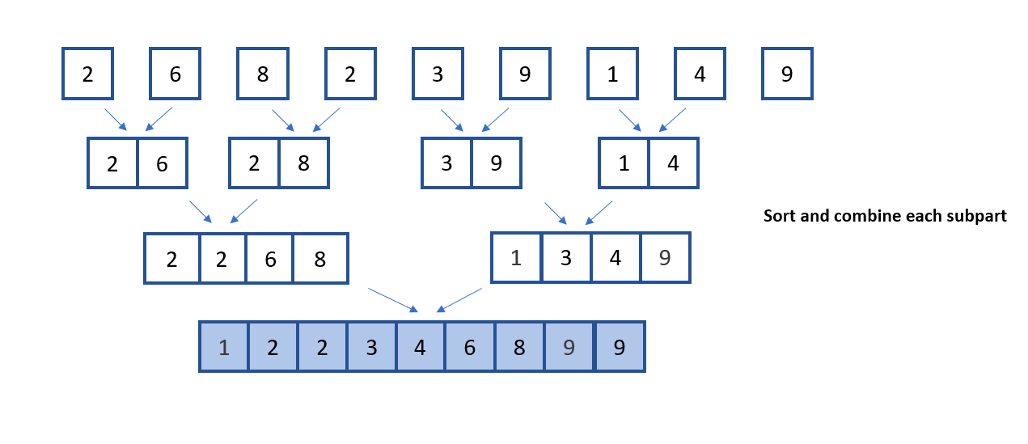
Мы разбиваем массив на две половины.
Мы рекурсивно сортируем каждую половину.
Мы объединяем отсортированные половины обратно вместе с помощью операции слияния.
Алгоритм сортировки слиянием (псевдокод)
function merge_sort(arr):
если длина arr <= 1:
возвращаем arr
mid = длина arr // 2
левая_часть = merge_sort(arr[:mid])
правая_часть = merge_sort(arr[mid:])
возвращаем merge(левая_часть, правая_часть)Заметим, что сложность операции слияния составляет \({\cal{O}(n)}\), так как мы проходим по всем элементам обоих массивов. Разбивать массив на две половины можно не более \(\log_2(n)\) раз.
Сложность такого алгоритма составляет:
\[ {\cal{O}(n \log n)} \]
Быстрая сортировка (quick sort)
Быстрая сортировка – это алгоритм вида “разделяй и властвуй”, который разбивает массив на две части на основе опорного элемента (pivot по-английски), где в левой половине хранятся элементы, меньше или равные опорному, а в правой – большие опорного. Операция такого разделения называется partition. Затем алгоритм быстрой сортировки рекурсивно сортирует каждую из частей.
Алгоритм partition (псевдокод)
Ниже приведен пример для Hoare partition.
функция partition(arr, l, r):
v = arr[(l + r) // 2]
i = l
j = r
пока i ≤ j:
пока arr[i] < v:
i = i + 1
пока arr[j] > v:
j = j - 1
если i ≥ j:
break
поменять местами arr[i] и arr[j]
i = i + 1
j = j - 1
вернуть jЭтот алгоритм работает следующим образом:
Мы выбираем опорный элемент
Идем с начала массва до тех пор, пока не найдем элемент, который больше опорного
Идем с конца массива до тех пор, пока не найдем элемент, который меньше опорного
Найденный элементы стоят не на своих местах, поэтому мы меняем их местами
Повторяем шаги 2-4 до тех пор, пока не дойдем до середины массива
После выполнения операции partition массив будет разбит на две части: элементы меньше или равные опорному и элементы больше опорного. Затем мы рекурсивно сортируем каждую из частей.
Алгоритм быстрой сортировки (псевдокод)
function quick_sort(a, l, r):
если l < r:
q = partition(a, l, r)
quick_sort(a, l, q)
quick_sort(a, q + 1, r)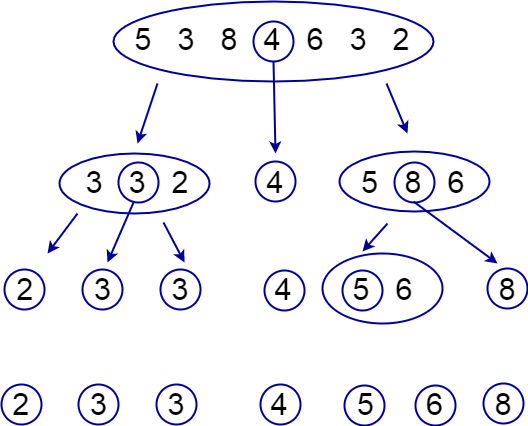
Сложность такого алгоритма в среднем составляет:
\[ {\cal{O}(n \log n)} \]
Важно отметить, что быстрая сортировка работает быстрее, чем сортировка слиянием, так как она использует меньше памяти. Это связано с тем, что быстрая сортировка работает на месте (in-place), то есть не требует дополнительной памяти для хранения промежуточных массивов.
Также можно понимать, что в худшем случае сложность быстрой сортировки составляет \({\cal{O}(n^2)}\), например, когда разбиение массива происходит неудачно и массив разбивается на две части, одна из которых содержит \(1\) элемент, а другая – \(n-1\) элементов. В этом случае быстрая сортировка будет работать так же, как сортировка выбором.
Интересно, что если способ выбора опорного элемента известен заранее, то всегда можно подобрать такой вход, что сложность сортировки будет квадратичной. Например, если мы всегда выбираем первый элемент массива в качестве опорного, то массив, отсортированный по убыванию, будет работать за \({\cal{O}(n^2)}\). В реальных задачах обычно используют случайный выбор опорного элемента, что позволяет избежать худшего случая.
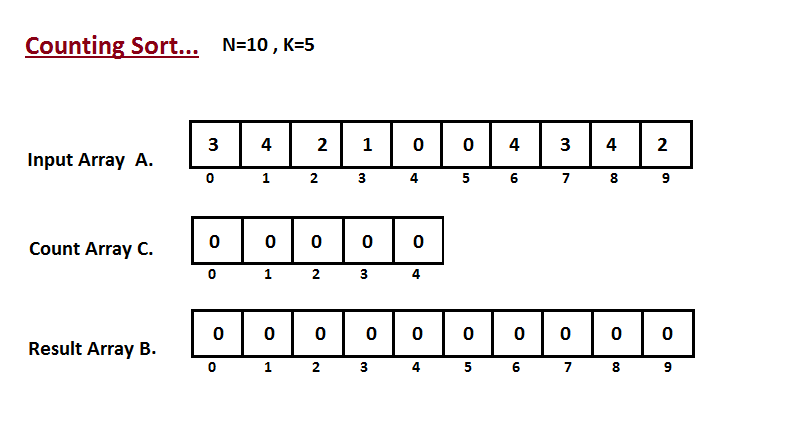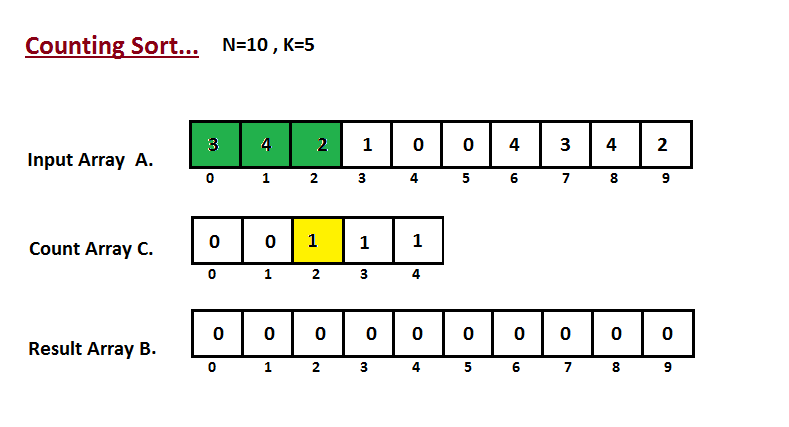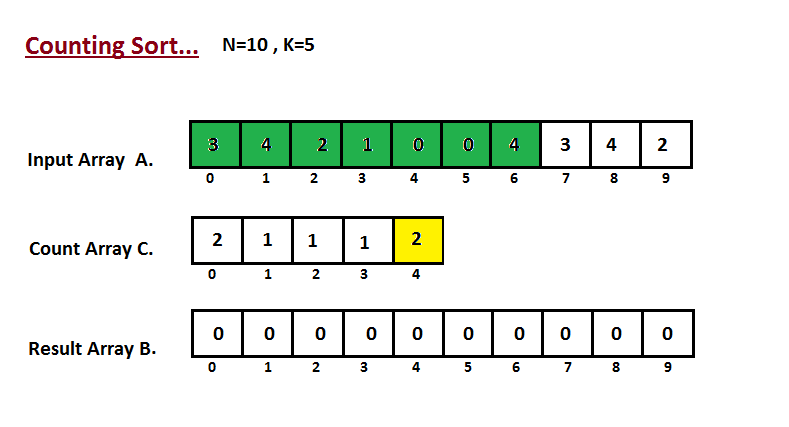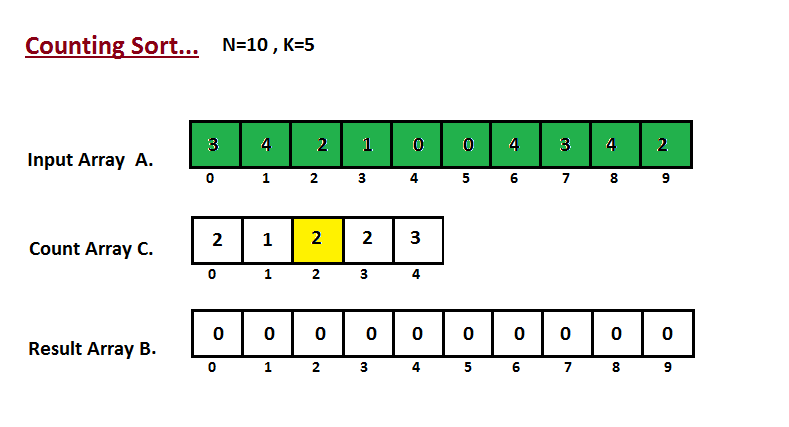
Сортировка подсчетом
Можно ли сделать сортировку быстрее, чем \({\cal{O}(n \log n)}\)? Можно! Но для этого потребуется иметь больше инструментов, чем единственный оператор “меньше”.
Все предыдущие алгоритмы работали с массивами, в которых лежат могут лежать абсолютно любые объекты, которые можно сравнивать: числа, строки, пары, другие массивы — почти все что угодно.
В особом случае, когда элементы могут принадлежать только какому-то небольшому множеству, можно использовать другой алгоритм — сортировку подсчетом (англ. counting sort).
Пусть, например, нам гарантируется, что все числа натуральные и лежат в промежутке от \(1\) до \(100\). Тогда есть такой простой алгоритм:
- Создадим массив размера \(100\), в котором будем хранить на \(k\)-ом месте, сколько раз число \(k\) встретилось в этом массиве.
- Пройдемся по всем числам исходного массива и увеличим соответствующее значение массива на \(1\).
- После того, как мы посчитали, сколько раз каждое число встретилось, можно просто пройтись по этому массиву и вывести \(1\) столько раз, сколько встретилась \(1\), вывести \(2\) столько раз, сколько встретилась \(2\), и так далее.
Время работы такого алгоритма составляет \(O(m + n)\), где \(m\) — число возможных значений, \(n\) — число элементов в массиве. Если количество возможных различных элементов в множестве относительно невелико, то сортировка подсчетом является одним из самых оптимальных решений.