Оценка сложности алгоритмов и
Оценка сложности алгоритмов
Чтобы оценить, насколько “сложной” для компьютера будет программа, насколько долго он будет ее считать, замерить время в секундах недостаточно: разные компьютеры обладают разной производительностью. Более того, время исполнения программы зависит от входных данных. Мы решим эту проблему подсчетом количества операций, которые наша программа будет совершать
Упрощенная модель
За 1 операцию будем считать:
арифметические операции (битовые операции тоже)
любое обращение к памяти (считаем, что все лежит в идеальной бесконечной RAM, из которой можно получить данные моментально)
доступ к элементу вектора
Модель действительно упрощена, ведь в реальном мире на все требуется реальное время, а память компьютера является неоднородной. Регистры процессора, L1-кэш, RAM, HDD/SDD – все это разная память с разными возможностями, но мы не будем их рассматривать, также как и случаи слишком больших данных (например, когда массив, который нужно обработать, невозможно полностью загрузить в RAM).
O-нотация
Для каждого алгоритма можно посчитать количество операций, оно будет зависеть от входных данных. Введем удобные обозначения для неточного восприятия функций
\(f(x) = {\cal{O}}(g(x)) \stackrel{def}{\Leftrightarrow} \exists C > 0: f(x) < C \cdot g(x)\)
Во всех дальнейших рассуждениях мы будем рассматривать все равенства и неравенства при больших \(x\) (более формально, \(x \to +\infty\)) и говорить об асимптотическом стремлении.
Такая запись позволяет легко определить рост функции: линейный, квадратичный, кубический, экспоненциальный, потому что только функций одной скорости асимтотического роста будет соблюдаться определение выше.
Пусть \(x \to +\infty\), тогда:
\(f(x) = x^3 + 2x^2 - 3x + 2 < x^3 + 2x^3 + 3x^3 + 2x^3 = 8x^3 \Rightarrow C = 8 > 0 \\ f(x) = x^3 + 2x^2 - 3x + 2 = {\cal{O}}(x^3)\)
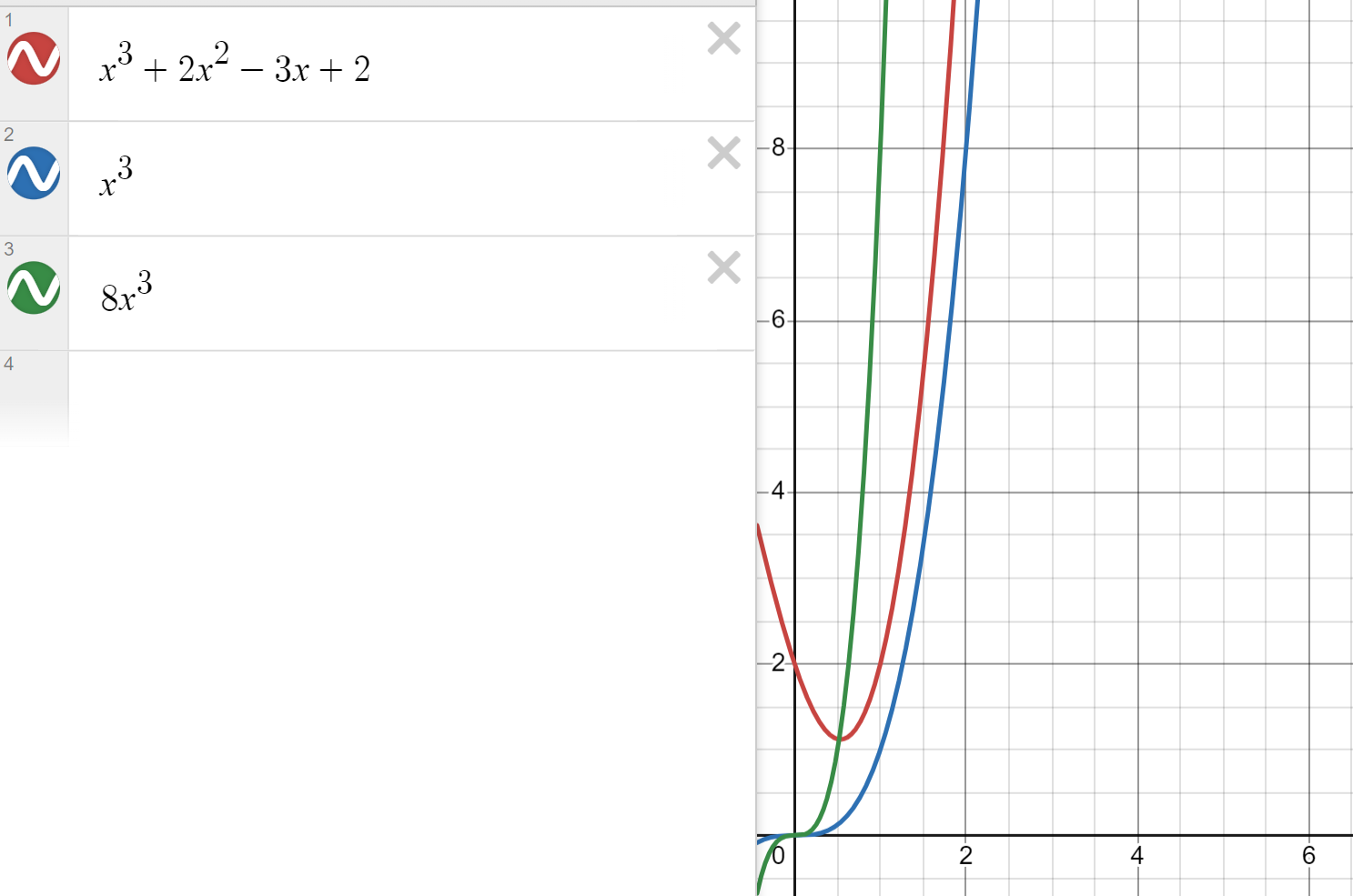
Несмотря на то что \(x^3\) меньше, чем \(f(x)\), нашелся константный множитель, с которым можно оценить нашу функцию \(f(x) < 8x^3\). Значит, рост кубический.
Рассмотрим на примерах:
Для большей связи с дальнейшим приложением можно считать, что функции подсчитывают количество операций, которые совершит наша программа.
\(f_1(n) = 1 + 2 + \dots + n = \frac{n(n + 1)}{2} = \frac{n^2}{2} + \frac{n}{2} < \frac{n^2}{2} + \frac{n^2}{2} = n^2 \Rightarrow f_1(n) = O(n^2)\)
\(f_2(n) = 1^2 + 2^2 + \dots + n^2 = \frac{n(n + 1)(2n + 1)}{6} = O(n^3)\)
Сложность пройденных задач
Разность между наибольшим и наименьшим значениями
За какую сложность можно найти разность между наибольшим и наименьшим значениями в некотором массиве из \(n\) элементов? Нам придется пройтись по всем элементам массива и на каждой итерации обновлять минимум и максимум. Главное, что мы будем знать их после такого прохода и сможем найти сумму. Это линейная сложность – \(O(n)\).
Покажем это более формально
#include <iostream>
#include <algorithm>
#include <vector>
int main() {
std::vector<int> data = {1, 2, 5, 2, 3, 1, -1, 5, 2, 1};
int max = data[0], min = data[0];
for (size_t i = 0; i < data.size(); ++i) {
max = std::max(max, data[i]);
min = std::min(min, data[i]);
}
printf("%d\n", max - min);
}На каждой итерации циклы мы проведем 2 сравнения, возможно, 1 присваивание. После цикла вычитание и вывод на экран. Покажем, почему такой мелкий подсчет количества операций неважен при обсуждении асимптотической сложности программы:
\(n \cdot (2 + 1) + 1 = 3n + 1 < 5n < 10n < 10^6 n = O(n)\)
При O-нотации мы можем опускать константы (см. формальное определение выше), а также не учитывать вклад младших степень – ведь он будет незначителен при “достаточно большом” \(n\) (\(n \to + \infty\))
Таким образом, программа выше обладает линейной сложность.
Количество единиц в двоичной записи
Какова сложность поиска всех цифр числа в двоичной записи? Например, какова сложность подсчета количества единиц?
Для этого вспомним код для такой задачи:
#include <iostream>
int main() {
int num;
std::cin >> num;
int cnt = 0;
while (num) {
cnt += num % 2;
num /= 2;
}
std::cout << cnt << '\n';
}Заметим, что на каждой итерации цикла число num уменьшает в 2 раза. В целых числах это можно сделать не более \(\log_2 n\) раз. Значит, наш алгоритм обладает логарифмической сложностью: \(O(\log n)\)
Стоит обратить внимание, что при указании асимптотической сложности нет смысла указывать основания логарифма, ведь рост любой логарифмической функции одинаков при больших \(n\). Это объясняется тем, что все логарифмы можно привести к одному основания умножение на константу, что там не важно по определению O-нотации
\(f_a(x) = \log_a x = \frac{\log_2 x}{\log_2 a} = \frac{1}{\log_2 a} \cdot \log_2 x = C \cdot \log_2 x = {\cal{O}}(\log x)\)
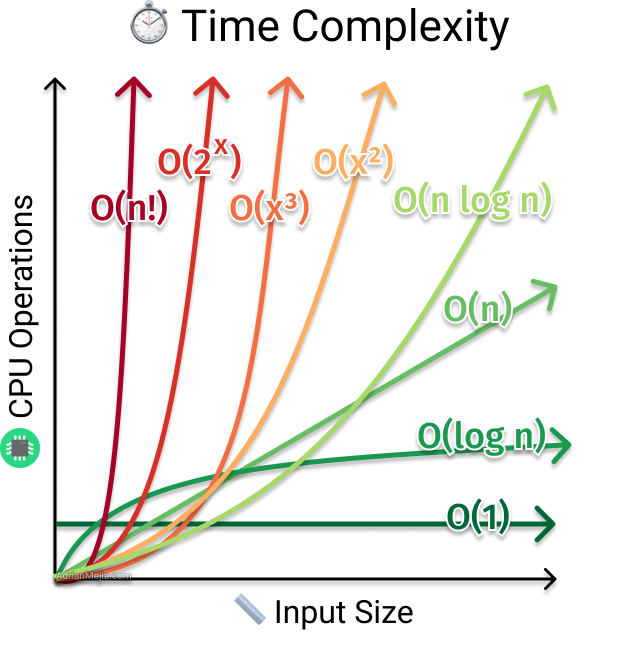
Какие сложности могут встретиться?
Сложности перечислены в порядке возрастания:
\({\cal{O}}(1)\) – константная сложность, то есть количество операций не зависит от входных данных
\({\cal{O}}(\log n)\) – логарифмическая сложность
\({\cal{O}}(\sqrt n)\)
\({\cal{O}}(n)\) – линейная сложность, “линия” – количество операций не более чем прямо пропорционально входным данным
\({\cal{O}}(n \log n)\) – квазилинейная сложность
\({\cal{O}}(n^2)\) – квадратичная, кубическая сложность. Здесь же будут все \({\cal{O}}(n^a)\), где \(a\) – это параметр
\({\cal{O}}(2^n)\) – экспоненциальная сложность. Здесь же будут все \({\cal{O}}(a^n)\), где \(a\) – это параметр
\({\cal{O}}(n!)\) – факториальная сложность
Быстрое возведение в степень
Наивный алгоритм возведение в степень будет работать за \(O(n)\): \(n\) раз нужно умножить на число.
Заметим, что:
\[ n \ \vdots \ 2 \Rightarrow a^n = a^{\frac{n}{2}} \cdot a^{\frac{n}{2}}, \text{где} \ \frac{n}{2} \in \mathbb{Z} \\ n \not{\vdots} \ 2 \Rightarrow a^n = a^{n - 1} \cdot a \]
Теперь напишем псевдокод для быстрого возведения числа num в степень deg. Будем считать, что все переменные корректно объявлены заранее
result = 1
пока deg != 0:
если deg четное, то
deg = deg / 2 # уменьшаем степень, в которую остально возвести, в 2 раза
num *= num # возводим текущее число в квадрат
если deg нечетно, то
deg -= 1
result *= num # умножаем на основание степени, на исходное число
теперь в result лежит num в степени degДля расчета асимптотической сложности заметим, что:
после обработки нечетного
deg, оно становится четным и на следующей итерации будет разделено на 2degуменьшается в 2 раза при каждом делении, а это, как мы уже знаем, может происходить не более \(\log_2 d\) раз
Тогда нашу сложность можно выразить как \(\log d + \log d\) = \(O(\log d)\) – логарифмическая сложность
Квадратичные сортировки
В этой главе нам предстоит формально определить сортировку элементов, обосновать нижнюю оценку на асимптотику и разобрать несколько алгоритмов сортировки, которые нужно будет самостоятельно реализовать.
Если не указано иное, то мы рассматривание объекты, для которых определен только оператор “меньше”. Это значит, чзто, имея \(a_1\) и \(a_2\), мы можно только определить истинности выражения \(a_1 < a_2\).
Сортировка – это процесс поиска такого расположения объектов, для которого будет выполняться введенное отношения порядка (\(\forall i < j \ : \ a_i < a_j\)). Формально сортировка – это поиск такой перестановки индексов, что \(a_{p_1} < a_{p_2} < ... < a_{p_n}\), где \(p\) – это перестановка индексов от 1 до n. Это наблюдение пригодится нам при доказательстве нижней оценки сложности алгоритмов сортировки.
Квадратичные сортировки
Сортировка пузырьком
Сортировка пузырьком – это алгоритм, который проходит по массиву и сравнивает соседние элементы. Если текущий элемент больше следующего, то они меняются местами. Алгоритм повторяет эту процедуру до тех пор, пока массив не будет отсортирован.
Допустим, у нас есть массив \([5, 3, 8, 4, 2]\).
| Шаг | Описание | Массив |
|---|---|---|
| 1 | Сравниваем 5 и 3. Поскольку 5 > 3, меняем их местами | \([3, 5, 8, 4, 2]\) |
| 2 | Сравниваем 5 и 8. Поскольку 5 < 8, ничего не меняем | \([3, 5, 8, 4, 2]\) |
| 3 | Сравниваем 8 и 4. Поскольку 8 > 4, меняем их местами | \([3, 5, 4, 8, 2]\) |
| 4 | Сравниваем 8 и 2. Поскольку 8 > 2, меняем их местами | \([3, 5, 4, 2, 8]\) |
| 5 | Повторяем процесс для всего массива | - |
В результате мы получаем отсортированный массив: \([2, 3, 4, 5, 8]\).

Важно понять, как и почему такой алгоритм действительно работает. Заметим, что на каждой итерации алгоритм “выталкивает” наибольший элемент в конец массива. Действительно, ведь такой элемент сможет “победить” во всех сравнениях с любым соседом, поэтому после его нахождения он начнет “всплывать” в конец массива. Таким образом, после первой итерации наибольший элемент оказывается в последней позиции, после второй итерации – на предпоследней и так далее. Это приводит к тому, что после \(i\)-той итераций последние \(i\) элементов массива уже отсортированы, значит, после \(n\) итераций массив будет отсортирован полностью.
Алгоритм (псевдокод)
function bubble_sort(arr):
n -- длина массива
arr -- массив, который нужно отсортировать
делаем n шагов
для i от 0 до n-1:
делаем n-i-1 шагов
для j от 0 до n-i-2:
если arr[j] > arr[j+1]:
меняем местами arr[j] и arr[j+1]
возвращаем arrСложность такого алгоритма составляет:
\[ {\cal{O}(n^2)} \]
Сортировка выбором
Сортировка выбором – это алгоритм, который проходит по массиву и находит минимальный элемент. Затем он меняет его местами с первым элементом массива. После этого алгоритм повторяет процесс для оставшейся части массива. Этот алгоритм работает аналогично сортировке пузырьком, но вместо того, чтобы “выталкивать” элементы, он “выбирает” минимальный элемент и помещает его на нужную позицию. Очевидно, что после \(n\) итераций массив будет отсортирован полностью.
Допустим, у нас есть массив \([5, 3, 8, 4, 2]\).
| Шаг | Описание | Массив |
|---|---|---|
| 1 | Находим минимальный элемент (2) и меняем его местами с первым элементом (5) | \([2, 3, 8, 4, 5]\) |
| 2 | Находим минимальный элемент (3) и меняем его местами со вторым элементом (3) | \([2, 3, 8, 4, 5]\) |
| 3 | Находим минимальный элемент (4) и меняем его местами с третьим элементом (8) | \([2, 3, 4, 8, 5]\) |
| 4 | Находим минимальный элемент (5) и меняем его местами с четвертым элементом (8) | \([2, 3, 4, 5, 8]\) |
В результате мы получаем отсортированный массив: \([2, 3, 4, 5, 8]\).
Алгоритм (псевдокод)
function selection_sort(arr):
n -- длина массива
arr -- массив, который нужно отсортировать
делаем n шагов
для i от 0 до n-1:
# находим индекс минимального элемента в оставшейся части массива
min_index = argmin(arr[i, i+1, i+2, ..., n-1])
меняем местами arr[i] и arr[min_index]
возвращаем arrСложность такого алгоритма составляет:
\[ {\cal{O}(n^2)} \]
Сортировка вставками
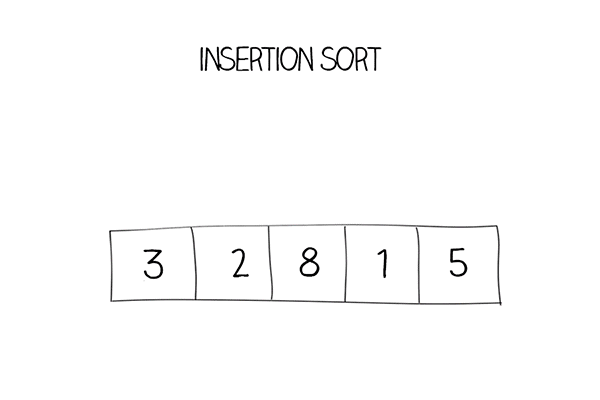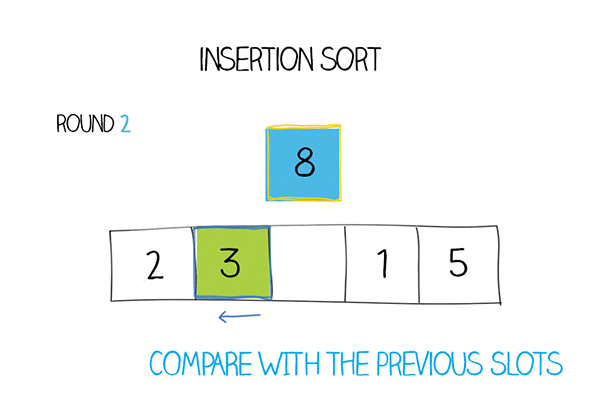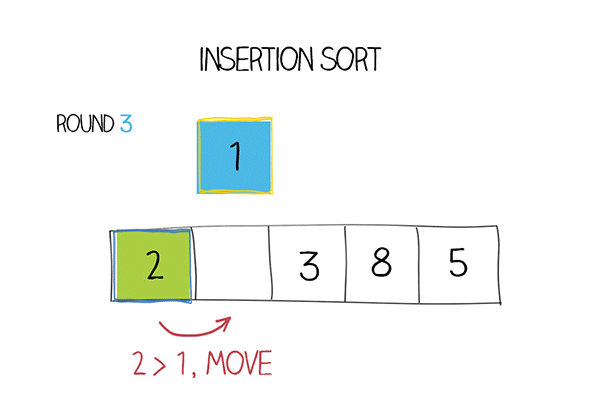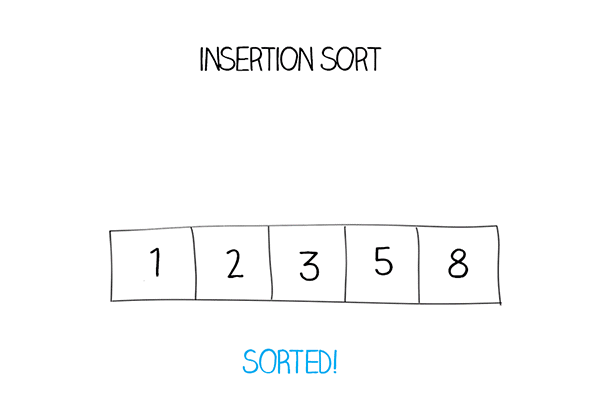
Сортировка вставками – это алгоритм, который проходит по массиву и на каждой итерации берет один элемент и вставляет его в правильную позицию среди уже отсортированных элементов.
Сначала алгоритм считает, что первый элемент массива уже отсортирован. Затем он проходит по остальным элементам и вставляет их в правильную позицию среди уже отсортированных элементов. Делается это путем сравнения текущего элемента с предыдущими и сдвигая элементы, которые больше текущего, на одну позицию вправо.
Допустим, у нас есть массив \([5, 3, 8, 4, 2]\).
| Шаг | Описание | Массив |
|---|---|---|
| 1 | Считаем, что первый элемент уже отсортирован | \([5]\) |
| 2 | Вставляем второй элемент (3) в правильную позицию | \([3, 5]\) |
| 3 | Вставляем третий элемент (8) в правильную позицию | \([3, 5, 8]\) |
| 4 | Вставляем четвертый элемент (4) в правильную позицию | \([3, 4, 5, 8]\) |
| 5 | Вставляем пятый элемент (2) в правильную позицию | \([2, 3, 4, 5, 8]\) |
В результате мы получаем отсортированный массив: \([2, 3, 4, 5, 8]\).
Алгоритм (псевдокод)
function insertion_sort(arr):
n -- длина массива
arr -- массив, который нужно отсортировать
делаем n шагов
для i от 1 до n-1:
key = arr[i]
j = i - 1
пока j >= 0 и arr[j] > key:
arr[j + 1] = arr[j]
j = j - 1
arr[j + 1] = key
возвращаем arrСложность такого алгоритма составляет:
\[ {\cal{O}(n^2)} \]