Обход в ширину
Поиск в ширину (англ. breadth-first search) — один из основных алгоритмов на графах, позволяющий находить все кратчайшие пути от заданной вершины и решать многие другие задачи.
Поиск в ширину также называют обходом — так же, как поиск в глубину и все другие обходы, он посещает все вершины графа по одному разу, только в другом порядке: по увеличению расстояния до начальной вершины.
Описание алгоритма
На вход алгоритма подаётся невзвешенный граф и номер стартовой вершины \(s\). Граф может быть как ориентированным, так и неориентированным — для алгоритма это не важно.
Основную идею алгоритма можно понимать как процесс «поджигания» графа: на нулевом шаге мы поджигаем вершину \(s\), а на каждом следующем шаге огонь с каждой уже горящей вершины перекидывается на всех её соседей, в конечном счете поджигая весь граф.
Если моделировать этот процесс, то за каждую итерацию алгоритма будет происходить расширение «кольца огня» в ширину на единицу. Номер шага, на котором вершина \(v\) начинает гореть, в точности равен длине её минимального пути из вершины \(s\).
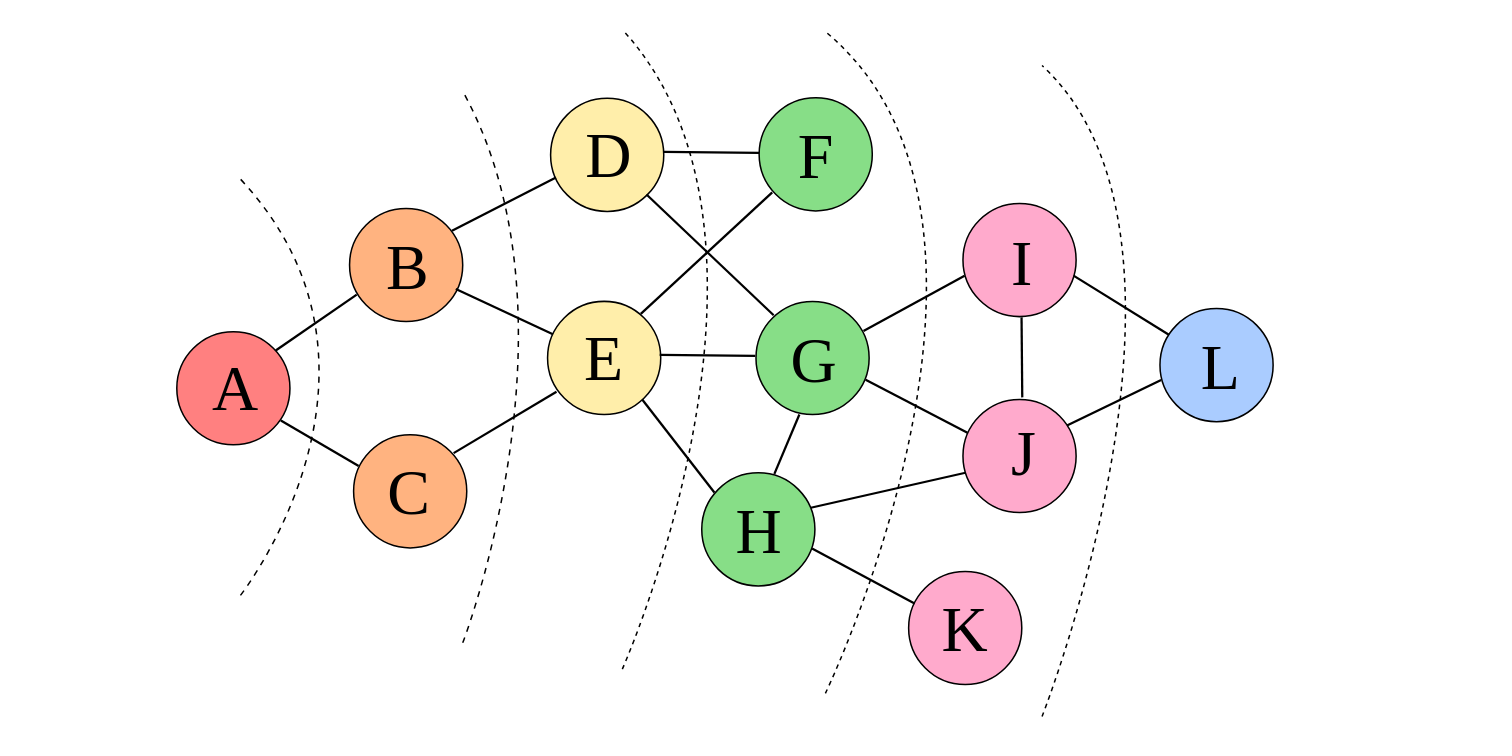
Моделировать это можно следующим образом. Создадим очередь, в которую будут помещаться горящие вершины, а также заведём булевый массив, в котором для каждой вершины будем отмечать, горит она или нет — или иными словами, была ли она уже посещена. Изначально в очередь помещается только вершина \(s\), которая сразу помечается горящей.
Затем алгоритм представляет собой такой цикл: пока очередь не пуста, достать из её головы одну вершину \(v\), просмотреть все рёбра, исходящие из этой вершины, и если какие-то из смежных вершин \(u\) ещё не горят, поджечь их и поместить в конец очереди.
В итоге, когда очередь опустеет, мы по одному разу обойдём все достижимые из \(s\) вершины, причём до каждой дойдём кратчайшим путём. Длины кратчайших путей можно посчитать, если завести для них отдельный массив \(d\) и при добавлении в очередь пересчитывать по правилу \(d_u = d_v + 1\). Также можно компактно сохранить дополнительную информацию для восстановления самих путей, заведя массив «предков», в котором для каждой вершины хранится номер вершины из которой мы в неё попали.
Реализация
Если мы всё равно поддерживаем массив расстояний, то отдельный булевый массив с метками горящих вершин можно не создавать, а вместо этого просто присвоить изначальное расстояние всех вершин некоторым некоторым специальным значением (например, -1), которое будет сигнализировать а том, что эту вершину мы ещё не просмотрели.
Дополняем нашу ООП реализацию графа:
#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
class Graph {
public:
Graph(int num_of_vertexes) {
n = num_of_vertexes;
data.resize(n);
visited.resize(n, false);
dists.resize(n, -1);
from_vertex.resize(n, -1);
}
void add_edge(int start, int stop) {
data[start].push_back(stop);
data[stop].push_back(start);
}
void BFS(int vertex) {
std::queue<int> vertexes_to_visit;
vertexes_to_visit.push(vertex);
while (!vertexes_to_visit.empty()) {
int current_vertex = vertexes_to_visit.front();
vertexes_to_visit.pop();
if (visited[current_vertex]) {
continue;
}
visited[current_vertex] = true;
std::cout << current_vertex << " ";
for (auto neig: data[current_vertex]) {
vertexes_to_visit.push(neig);
dists[neig] = dists[current_vertex] + 1; // or weight of edge in case of weighted graph
from_vertex[neig] = current_vertex;
}
}
}
void print_path(int start, int stop) {
if (dists[stop] == -1) {
std::cout << "No path from " << start << " to " << stop << '\n';
return;
}
std::vector<int> path;
int current_vertex = stop;
while (current_vertex != start) {
path.push_back(current_vertex);
current_vertex = from_vertex[current_vertex];
}
path.push_back(start);
std::reverse(path.begin(), path.end());
for (auto vertex: path) {
std::cout << vertex << " ";
}
std::cout << '\n';
}
int n = 0;
std::vector<std::vector<int>> data;
std::vector<bool> visited;
std::vector<int> dists;
std::vector<int> from_vertex;
};Стоит обратить внимание, что одновременно с обходом графа заполняются 2 массива:
from_vertex– откуда приходили в каждую из вершин, будем использовать для восстановления путиdists– главный идейный массив обхода, так как заполняем его расстояниями от начальной вершины обхода до всех достижимых вершин графа
В неявных графах
Поиск в ширину часто применяется для поиска кратчайшего пути в неявно заданных графах.
В качестве конкретного примера, пусть у нас есть булева матрица размера \(n \times n\), в которой помечено, свободна ли клетка с координатами \((x, y)\), и требуется найти кратчайший путь от \((x_s, y_t)\) до \((x_y, y_t)\) при условии, что за один шаг можно перемещаться в свободную соседнюю по вертикали или горизонтали клетку.

Можно сконвертировать граф в явный формат: как-нибудь пронумеровать все ячейки (например по формуле \(x \cdot n + y\)) и для каждой посмотреть на всех её соседей, добавляя ребро в \((x \pm 1, y \pm 1)\), если соответствующая клетка свободна.
Такой подход будет работать за оптимальное линейное время, однако с точки зрения реализации проще адаптировать не входные данные, а сам алгоритм обхода в глубину:
bool a[N][N]; // свободна ли клетка (x, y)
int d[N][N]; // кратчайшее расстояние до (x, y)
// чтобы немного упростить код
struct cell {
int x, y;
};
void bfs(cell s, cell t) {
queue<cell> q;
q.push(s);
memset(d, -1, sizeof d);
d[s.x][x.y] = 0;
while (!q.empty()) {
auto [x, y] = q.front();
q.pop();
// просматриваем всех соседей
for (auto [dx, dy] : {{-1, 0}, {+1, 0}, {0, -1}, {0, +1}}) {
// считаем координаты соседа
int _x = x + dx, _y = y + dy;
// и проверяем, что он свободен и не был посещен ранее
if (a[_x][_y] && d[_x][_y] == -1) {
d[_x][_y] = d[x][y] + 1;
q.push_back({_x, _y});
}
}
}
} Перед запуском bfs следует убедиться, что не произойдет выход за пределы границ. Вместо того, чтобы добавлять проверки на _x < 0 || x >= n и т. п. при просмотре возможных соседей, удобно сделать следующий трюк: изначально создать матрицу a с размерностями на 2 больше, чем нужно, и на этапе чтения данных заполнять её в индексации не с нуля, а с единицы. Тогда границы матрицы всегда будут заполнены нулями (то есть помечены непроходимыми) и алгоритм никогда в них не зайдет.
Применения и обобщения
Ребра на кратчайшем пути. Мы можем за линейное время найти все рёбра, лежащие на каком-либо кратчайшем пути между заданной парой вершин \(a\) и \(b\). Для этого нужно запустить два поиска в ширину: из \(a\) и из \(b\).
Обозначим через \(d_a\) и \(d_b\) массивы кратчайших расстояний, получившиеся в результате этих обходов. Тогда каждое ребро \((u,v)\) можно проверить критерием
\(d_a[u] + d_b[v] + 1 = d_a[b]\)
Альтернативно, можно запустить один обход из \(a\), и когда он дойдет до \(b\), начать рекурсивно проходиться по всем обратным ребрам, ведущим в более близкие к \(a\) вершины (то есть те, для которых \(d[u] = d[v] - 1\)), отдельно помечая их.
Аналогично можно найти все вершины на каком-либо кратчайшем пути.
0-1 BFS. Если веса некоторых ребер могут быть нулевыми, то кратчайшие пути искать не сильно сложнее.
Ключевое наблюдение: если от вершины \(a\) до вершины \(b\) можно дойти по пути, состоящему из нулевых рёбер, то кратчайшие расстояния от вершины \(s\) до этих вершин совпадают.
Если в нашем графе оставить только \(0\)-рёбра, то он распадётся на компоненты связности, в каждой из которых ответ одинаковый. Если теперь вернуть единичные рёбра и сказать, что эти рёбра соединяют не вершины, а компоненты связности, то мы сведём задачу к обычному BFS.
Получается, запустив обход, мы можем при обработке вершины \(v\), у которой есть нулевые ребра в непосещенные вершины, сразу пройтись по ним и добавить все вершины нулевой компоненты, проставив им такое же расстояние, как и у \(v\).
Это можно сделать и напрямую, запустив BFS внутри BFS, однако можно заметить, что достаточно при посещении вершины просто добавлять всех её непосещенных соседей по нулевым ребрам в голову очереди, чтобы обработать их раньше, чем те, которые там уже есть. Это легко сделать, если очередь заменить деком:
vector<int> d(n, -1);
d[s] = 0;
deque<int> q;
q.push_back(s);
while (!q.empty()) {
int v = q.front();
q.pop_front();
for (auto [u, w] : g[v]) {
if (d[u] == -1) {
d[u] = d[v] + w;
if (w == 0)
q.push_front(u);
else
q.push_back(u);
}
}
}Также вместо дека можно завести две очереди: одну для нулевых ребер, а другую для единичных, в внутри цикла while сначала просматривать первую, а только потом, когда она станет пустой, вторую. Этот подход уже можно обобщить.